Aviso: O conteúdo aqui apresentado tem uma finalidade exclusivamente informativa sobre um tipo específico de jogo e como jogá-lo. O objetivo deste conteúdo não é nem promover nem disponibilizar um tipo de jogo, mas simplesmente informar o jogador acerca de como jogá-lo.
__________________________________________
Henry Poincaré
Sumário
Como calcular as probabilidades da roleta
- Introdução
- A fórmula matemática para calcular a probabilidade
- Exemplo de alterações simples
- Exemplo das Dúzias
- Exemplo com um Número
- Um número que se repete 3 vezes em 38 jogadas na roleta americana
- Conclusão
INTRODUÇÃO
É essencial para qualquer jogador conhecer as probabilidades dos jogos de casino. As probabilidades na roleta não precisam necessariamente de ser um bicho de 7 cabeças. Sim, é normal que possa existir alguma matemática pelo meio mas tal não significa que precise começar já a fugir a 7 pés. Este artigo visa dar alguma luz sobre as probabilidades na roleta com algumas dicas mais simples e algumas fórmulas mais avançadas que poderão ser a chave para si e para melhorar o seu jogo de roleta. Aliás, todos sabemos que a matemática no casino é imprescindível se quer vencer.
Para começar, tudo depende da aposta efetuada. Assim, vamos começar por explicar que as apostas internas apresentam uma probabilidade menor, mas a taxa de pagamento é superior enquanto que as apostas externas segue na direção inversa.
Sempre que puder, escolha a roleta europeia pois ao apresentar um único 0, torna-se mais rentável. A versão americana detém o 0 e o 00. Pode parecer pouco mas tal traduz-se numa vantagem para a casa de 2,70% na variante europeia e 5,26% na vertente americana. Já está a começar a fazer contas? Calma, vamos continuar.
Se quiser jogar pelo seguro, saiba que as apostas externas são menos arriscadas nas duas variantes da roleta. Por outras palavras, ao apostar tanto no preto como no vermelho, você tem praticamente 50% de hipóteses de ganhar.
Mais uma vez, as apostas internas vão em sentido oposto. Se por um lado apresentam percentagens menos boas, por outro lado dão mais dinheiro. Colocando estas palavras em números, a quota de uma aposta interna num número é somente de 1 contra 37%, contudo se a bola parar no número de eleição, você ganha 35 vezes o valor da aposta inicial! Nada Mau!
Tudo o que foi dito acima é verdade do ponto de vista matemático, mas vamos continuar com o artigo no nosso casino blog para elementos mais profundos sobre as fórmulas que podem desbloquear as probabilidades na roleta.
Apesar de toda a discussão sobre probabilidades e estatísticas, parece que poucas pessoas conseguem calcular matematicamente a probabilidade de um determinado resultado na roleta. Às vezes, as pessoas recorrem ao excel ou usam programas especializados, tentando testar milhões de jogadas para obter o número certo. Quando alguém entende a probabilidade básica, pode-se responder a quase todas as perguntas sobre a certeza de qualquer resultado utilizando apenas uma simples calculadora ou simplesmente colocar a equação como uma fórmula num ficheiro excel. As probabilidades fazem parte da roleta, até mesmo de uma roleta de shots, portanto, não vale a pena fugir!
Primeiro de tudo, temos de entender qual é a função factorial, que tem o símbolo: !
Tal significa multiplicar uma série de números naturais descendentes.
Exemplos:
- 4! = 4 × 3 × 2 × 1 = 24
- 7! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040
- 1! = 1
- 0!=1 (obviamente)
Para fins da roleta de casino, um factorial mostra de quantas maneiras diferentes, diferentes itens (ou números) podem ser organizados. Sem repetições do mesmo item ou número. Para ter uma ideia de quão grande esse número pode ser, vamos ao caso de 37 números, como na roleta europeia:
37! = 1,3763753×1043
Tal significa que existem triliões de triliões de disposições diferentes a partir dos 37 números da roleta. Isto sem contar com as possíveis repetições de números. De quantas maneiras diferentes (sequências) todos os números da roleta podem aparecer em 37 jogadas? Poderá ler mais sobre combinações matemáticas aqui.
A EQUAÇÃO DA PROBABILIDADE
Eis a principal fórmula matemática para calcular a probabilidade de qualquer resultado ou ocorrência na roleta...
Em primeiro lugar, devemos definir os parâmetros:
- P(e) é a probabilidade de um evento E.
- n é o número de tentativas (jogadas)
- x é o número de vezes que a nossa aposta ganha
- P(b) é a probabilidade da nossa aposta B ganhar numa jogada
A probabilidade P(e) do evento E = [ Aposta b aparecer x vezes em n jogadas ] =
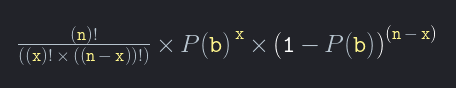
mais uma vez:
P(e) = (n!/(x!(n-x)!)) P(b)x (1-P(b))n-x
Se deseja entender um pouco melhor esta equação, poderá pesquisar a distribuição binomial, que é a base da maioria das probabilidades de roleta. É bom também enfatizar a importante diferença entre probabilidade e expectativa. Aqui está um método rápido e fácil para calcular o risco na roleta e este artigo vai ajudá-lo a entender e calcular o valor esperado de qualquer aposta.
Vamos agora ver o quão poderoso este método é em ação. Os exemplos a seguir vão ajudá-lo a entender melhor como a fórmula funciona.
EXEMPLO DE ALTERAÇÕES SIMPLES
Digamos que quer calcular a probabilidade de dois números pretos em três jogadas. Ou, de maneira diferente, “com que frequência veremos exatamente dois números pretos em três jogadas”. Observe que esta equação calcula as probabilidades exatas de um evento específico. Não são as probabilidades de 2 ou mais pretos, mas exatamente 2 pretos.
Os parâmetros são:
- n = 3 (total de jogadas)
- x = 2 (números pretos/ jogadas vencedoras)
- P(b) = 0,5 (a probabilidade de sair Preto em cada rodada – ignoramos o zero para simplificar)
P(e) = (3!/(2!(3-2)!)) 0,52 (1-0,5)3-2
P(e) = (3!/(2!1!)) 0,52 0,51
P(e) = (3×2×1/2×1×1) 0,25× 0,5
P(e) = (3/1) 0,25× 0,5
P(e) = 3 × 0,125 = 0,375
Assim, a probabilidade em 3 jogadas de ter exactamente 2 números Pretos é 0,375 ou 37,5% ou um pouco mais de 1/3. Todos estes números são apenas expressões diferentes da mesma coisa: a expectativa do acontecimento do mesmo evento.
EXEMPLO DAS DÚZIAS
Queremos calcular a probabilidade de uma dúzia específica (não uma qualquer) sair exatamente 2 vezes em 6 jogadas.
- n = 6
- x = 2
- P(b) = 12/37
P(e) = (6×5×4!/(2!4!)) 0,3242 0,6764
P(e) = (30/2) 0,105× 0,209
P(e) = 15 × 0,022
P(e) = 0,329 ou 32,9% ou cerca de 1/3
EXEMPLO COM UM NÚMERO
Sabe que na roleta europeia, a probabilidade de um número específico aparecer numa jogada é 1/37 ou 2,7%. Mas qual é a probabilidade de um número específico aparecer exatamente 1 vez em 37 jogadas?
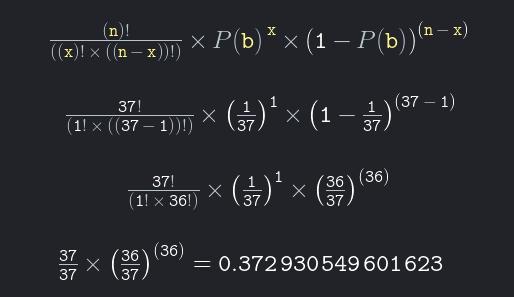
A probabilidade de um número específico aparecer exatamente uma vez no decorrer de 37 jogadas é de 0,373 ou 37,3%.
Utilizando a mesma fórmula, podemos calcular a probabilidade de um número específico não aparecer em todas as 37 jogadas (0,362 ou 36,2%) e a probabilidade dele aparecer duas vezes (0,186 ou 18,6%). A fórmula matemática que apresentamos aqui pode ser aplicada para encontrar quaisquer probabilidades de roleta na forma de de “Aposto que B sai X vezes em N jogadas”.
UM NÚMERO QUE SE REPETE 3 VEZES EM 38 JOGADAS NA ROLETA AMERICANA
Ao inserir os valores relevantes na equação principal, obtemos:
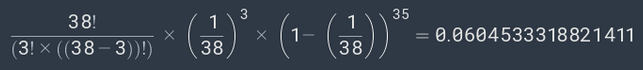
O que significa que a probabilidade disso acontecer é 0,06 ou 6% ou 1/16,6.
Consequentemente, podemos esperar que um fenómeno como este aconteça uma vez em 633 jogadas. Como em 38 jogadas isso tem probabilidades de 1/16,6, podemos esperar que ocorra, em média, depois de 38*16,6 = 633 jogadas.
Apresentamos aqui uma útil calculadora de probabilidades roleta para estes jogos, onde pode COPIAR e COLAR a EQUAÇÃO e depois aplicar os números.
Saiba mais em Khan Academy
PONTOS-CHAVE
- Existem triliões de triliões de disposições diferentes a partir dos 37 números da roleta.
-
Equação da Probabilidade: A probabilidade P(e) do evento E = [ Aposta b aparecer x vezes em n jogadas ] =
-
É possível efetuar alterações simples à equação e assim ajustá-la à realidade em questão. Tal é igualmente possível com dúzias e um único número.
