Aviso: O conteúdo aqui apresentado tem uma finalidade exclusivamente informativa sobre um tipo específico de jogo e como jogá-lo. O objetivo deste conteúdo não é nem promover nem disponibilizar um tipo de jogo, mas simplesmente informar o jogador acerca de como jogá-lo.
Artigo atualizado a 23 de Fevereiro de 2024
Compreender a estatística utilizada pelos casinos é essencial para avaliar resultados. Usamos esta avaliação para determinar se os resultados, bons ou maus, são em função da sorte ou da habilidade. Neste artigo, vou aplicar a análise estatística ao blackjack. Mas, sem muito esforço, isto pode ser aplicado a qualquer jogo de casino.
O blackjack não adere às leis matemáticas tradicionais do jogo. A maioria dos jogos de sorte e azar refletem o conceito matemático conhecido como “a lei das tentativas independentes”, que afirma que eventos passados não têm impacto em eventos futuros.
Se uma moeda for atirada ao ar, há 50% de probabilidade de o resultado ser cara e 50% de probabilidade de o resultado ser coroa. Se sair cara 10 vezes seguidas, o lançamento seguinte voltaria a ter 50% de probabilidade de sair cara. No blackjack, aquilo que acontece no passado afeta diretamente o que acontece no futuro. O blackjack tem memória e a lei das tentativas independentes não é válida.
Um Olhar Sobre as Vantagens
Quando uma pessoa sai de um casino, a pergunta que inevitavelmente surge na sua mente é "Porque é que perdi?". A maioria das pessoas que jogam em casinos são jogadores perdedores. Isso acontece porque a maioria dos jogos de casino, por natureza, têm uma expectativa negativa para o jogador. Isso significa que, para cada aposta feita no jogo, seja numa máquina ou numa mesa de jogo, o retorno ao longo do tempo é inferior ao valor apostado.
Se 1 milhão de jogadores apostarem 1 euro e um jogador ganhar 500 mil euros, o casino obtém um lucro de 500 mil euros e é percebida uma perda média de 50 cêntimos por aposta. Nas slot machines, o retorno anunciado muitas vezes ronda os 97-99%. Isso é ao longo de toda a vida útil da máquina, onde uma máquina pode recolher centenas de milhões de euros em apostas durante a sua existência. Os jogos de mesa são ligeiramente diferentes porque alguns incluem um componente de habilidade e a vantagem percentual que o casino tem varia de jogador para jogador. Mas aplica-se o mesmo princípio geral.
No blackjack, cada carta tem um valor específico que é adicionado ou subtraído da vantagem inicial que o casino tem sobre o jogador. Quando um número suficiente de cartas certas é distribuído, a vantagem passa para o lado do jogador. Isso é alcançado ao somar as vantagens sobre todas as possibilidades. Por exemplo, se uma mão tem uma vantagem positiva de 5% e outra mão tem uma vantagem de -6%, então a vantagem total para as duas mãos é de +1%. Quando o leitor compreender este jogo (para além das regras do mesmo), será fácil traduzir os conceitos para qualquer outro jogo de casino com uma vantagem estática sobre o jogador.
Quando um Ás ou uma carta de valor 10 é distribuída, a vantagem do casino no blackjack sobre o jogador aumenta. Quando cartas de valor mais baixo são colocadas em jogo, a vantagem do casino diminui, e quando um número suficiente dessas cartas é distribuído, o jogador tem uma vantagem sobre o casino.
Quando sobra uma abundância de cartas altas, o jogador tem uma vantagem sobre o casino. Isso acontece por vários motivos. Primeiro, blackjacks acontecem com mais frequência e, como o pagamento de um blackjack é assimétrico (o jogador recebe 3:2 quando faz blackjack, mas apenas perde a sua aposta inicial quando o dealer tem blackjack), o jogador sai beneficiado.
Em segundo lugar, algumas das opções do jogador tornam-se mais valiosas, como abrir ou dobrar. Normalmente, um jogador quer ver uma carta alta virar quando dobra ou abre a sua mão. Ou então dá uso a estas opções quando o dealer está fraco e é provável que uma carta alta faça o dealer rebentar.
Estas jogadas têm um retorno mais alto quando o baralho é rico em cartas altas. Por fim, o jogador pode variar a sua estratégia dependendo da composição das restantes cartas. Com uma preponderância de cartas altas, o jogador pode não pedir carta com mãos mais complicadas (totais de 12 a 16), dobrar mais vezes com totais fortes ou quando o dealer está fraco e suscetível a ultrapassar 21. Por outro lado, as regras proíbem o dealer de variar a sua estratégia.

Pensando nos Números
Compreender as estatísticas envolvidas nos jogos de casino é essencial para avaliar os resultados. Esta afirmação é válida tanto para o jogador como para os casinos. O conhecimento apresentado aqui é necessário para determinar se os resultados, quer sejam bons ou maus, estão dentro do domínio estatístico da possibilidade.
A maioria dos jogos de sorte e azar refletem o conceito matemático conhecido como "a lei das tentativas independentes". Esse conceito afirma que eventos passados não têm relevância nos eventos futuros. Isso é facilmente evidenciado na Roleta e em Craps.
Uma estratégia de blackjack que dá uma vantagem de 1% significa que por cada mão de blackjack que é jogada por €100, o Expected Value (EV) [Valor Esperado] é €1. Este valor é calculado utilizando a equação de expected value na equação 1.
EV = TAMANHO DA APOSTA (X) % VANTAGEM (X) # MÃOS JOGADAS
Equação 1
Se aplicarmos o cenário de valor expectável ao lançamento de uma moeda, sabemos que há dois lados numa moeda e, portanto, temos 50% de probabilidade de acertar cara e 50% de probabilidade de acertar coroa. Por isso, a equação que nos diz quantas vezes devemos esperar cara em 100 lançamentos de uma moeda é a Equação 2. Esta é uma equação de variável única e o tamanho da aposta pode ser igual a 1.
EV = ½ (X) 100
Equação 2
Quando uma moeda é lançada ao ar 100 vezes, o resultado raramente é 50 vezes cara e 50 vezes coroa. Posto isto, temos de introduzir o conceito de variância por número de eventos. A variância é uma medida de dispersão estatística. Em termos leigos, diz-nos o quão longe do valor esperado o resultado de uma tentativa ou experiência pode ficar.
Para nos mantermos no exemplo do lançamento da moeda ao ar, a variância ajuda a responder à pergunta se será, ou não, surpreendente se virmos 45 vezes cara em 100 lançamentos, ou se virmos apenas 5 vezes cara em 100 lançamentos. As respostas são não e sim, respetivamente. Sair cara apenas cinco vezes em 100 lançamentos provaria, virtualmente, que você estava a atirar ao ar uma moeda mais pesada de um lado do que do outro.
Compreender este conceito é crucial, pois é necessária uma correta análise estatística para determinar se os resultados (bons ou maus) são em função da sorte ou da habilidade.

Em Que Medida é o Blackjack Diferente?
No Blackjack, cada carta tem um valor específico que adiciona ou subtrai da vantagem inicial que o casino tem sobre o jogador. A vantagem inicial deriva das regras do jogo. Quando certas cartas suficientes são distribuídas, a vantagem inclina-se a favor do jogador. No blackjack, quando um Ás ou uma carta de valor 10 é distribuída, a vantagem do casino sobre o jogador aumenta. Quando cartas de valor mais baixo entram em jogo (2-7), a vantagem do casino diminui, e quando cartas suficientes dessas são distribuídas, o jogador tem uma vantagem sobre o casino.
A vantagem percentual que o casino tem sobre o jogador (no blackjack) ou vice-versa não é estática. Existem várias abordagens que se podem introduzir para acompanhar as percentagens em mudança. A mais simples, e a que está menos sujeita a erros por parte do jogador, é o sistema de contagem Alto/Baixo. Este sistema atribui valores de 1, -1 ou 0 às cartas. Todas as cartas de 2 a 6 recebem um valor de 1, e todas as cartas com um valor facial de 7, 8 e 9 têm um valor de 0. Todas as cartas com valor de dez, cartas de figuras e Ás têm um valor de -1. À medida que as cartas são distribuídas, o jogador soma os valores atribuídos às cartas e a soma destas cartas após uma ronda de blackjack é denominada contagem corrente.
Numa contagem corrente positiva, o valor é normalizado numa média de quantas cartas altas há a mais do que cartas baixas (ou cartas baixas a mais do que cartas altas) por baralho. Para isso, o jogador estima quantos baralhos ainda estão por jogar, e a contagem corrente é então dividida pelo número de baralhos restantes, sendo este valor denominado por contagem verdadeira. Por exemplo, se um jogador concluiu que três baralhos de um sapato de seis baralhos foram jogados, e a contagem corrente é 15, isso significa que quinze cartas baixas (2-6) foram jogadas a mais do que cartas altas (10s, cartas de figuras e ases) nos primeiros três baralhos do sapato; então, o jogador pega na contagem corrente (15) e divide pelos baralhos restantes (3), o que daria uma contagem verdadeira de 5.
O jogador subtrai uma compensação: geralmente 1, que leva em consideração a vantagem do casino no início do baralho ou sapato (esta compensação depende de vários fatores, como as regras do blackjack e o número de baralhos utilizados), e esse número é o número de unidades que o jogador apostaria na próxima mão. Para cada incremento de unidade inteira (positivo ou negativo) observado na contagem verdadeira, a vantagem do jogador aumenta aproximadamente 0.5%, positivos ou negativos, respetivamente.
Quando há uma predominância de cartas altas, a contagem verdadeira é alta e o jogador tem vantagem sobre o casino. Isso ocorre por três razões. Primeiro, os blackjacks são distribuídos com mais frequência e, como o pagamento de um blackjack é assimétrico (o jogador recebe 3:2 quando completa um blackjack, mas perde apenas a aposta inicial quando o dealer completa um blackjack), isso beneficia o jogador. Em segundo lugar, algumas opções dos jogadores tornam-se mais valiosas, como dividir e dobrar.
Normalmente, um jogador gostaria de ver uma carta alta sair ao dobrar ou dividir, ou o jogador exerce essas opções quando o dealer está fraco e uma carta alta fará o dealer rebentar (uma carta que faria o dealer ultrapassar 21). Essas jogadas têm um retorno maior quando o baralho restante é rico em cartas altas.
Por fim, o jogador pode variar a sua estratégia dependendo da composição das cartas restantes. Com uma predominância de cartas altas, o jogador pode ficar em mais mãos difíceis (totais de 12-16), dobrar mais vezes com totais fortes (cartas iguais a 9, 10 ou 11) ou, quando o dealer está fraco e propenso a ultrapassar 21, o jogador pode ficar. Em contraste, as regras proíbem o dealer de variar a sua estratégia. A combinação desses fatores cria situações em que a vantagem do casino é superada e um jogador habilidoso tem vantagem sobre a casa.
Se isto lhe parece complexo e quer apanhar um atalho, leia o nosso artigo sobre índices do blackjack e pense duas vezes.
Um Olhar Sobre a Variância
Quando uma moeda é lançada 100 vezes, o resultado raramente é exatamente 50 vezes cara e 50 vezes coroa. Portanto, devemos introduzir o conceito de variância por número de eventos. A variância é uma medida de dispersão estatística. Em termos leigos, lida com o quão longe do valor esperado o resultado de uma tentativa ou experiência pode estar.
A variância nos jogos de casino é normalmente discutida em termos de desvios padrão e será esse o caso daqui para a frente nesta discussão. O desvio padrão é simplesmente a raiz quadrada da variância. O desvio padrão para uma série de tentativas é dado pela Equação 3.
Desvio Padrão = (Desvio Padrão para um único evento) X (Número de Eventos)^(1/2)
Equação 3
A figura seguinte mostra o quão provável é os resultados caírem dentro de um, dois ou três desvios padrão do resultado esperado. Na representação gráfica, o valor esperado é indicado pela letra grega MU e o Desvio Padrão é representado pela letra grega SIGMA.
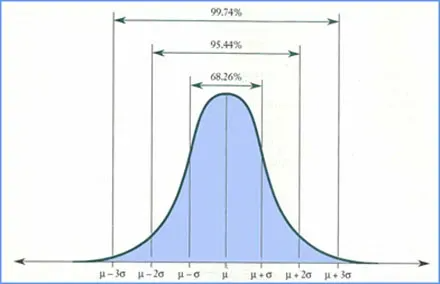
De acordo com a curva de distribuição de Gaussian (distribuição normal), há pouco mais de 68% de probabilidade de o resultado estar dentro de um desvio padrão, mais ou menos do valor esperado. Há pouco mais de 95% de probabilidade de o resultado estar dentro de dois desvios padrão, mais ou menos do valor esperado. Há uma probabilidade de, aproximadamente, 100% de os resultados estarem dentro de três desvios padrão a qualquer momento.
Aplicando isto ao cenário de 100 lançamentos de uma moeda ao ar, concluímos que o desvio padrão para 100 tentativas é 10 vezes o desvio padrão de uma única tentativa (que é 0.5), o que resulta num desvio padrão de 5 na experiência de 100 lançamentos.
No cenário de moeda ao ar, esperamos que 50 dos 100 lançamentos sejam cara e 50 coroa. Incluindo o conceito de desvio padrão de +/- 5, há uma probabilidade de 68% de que em 100 lançamentos de uma moeda ao ar, os resultados pendam entre 45 e 55 para cada um dos lados.
Há uma probabilidade de 95% de que o número de caras esteja entre 40 e 60 (2 * σ) e uma probabilidade de 99,9% de que o número de caras fique entre 35 e 65 (3 * σ).
Aplicando as equações de valor esperado e desvio padrão à unidade de aposta de 100 euros para um jogo de casino com uma vantagem de 1% sobre o jogador, os seguintes resultados são calculados:
| # de Mãos | Valor Esperado | Desvio Padrão |
| 100 | 100 | +/- 1,100 |
| 10,000 | 10,000 | +/- 11,000 |
| 1,000,000 | 1,000,000 | +/- 110,000 |
Graficamente, é representado da seguinte forma:
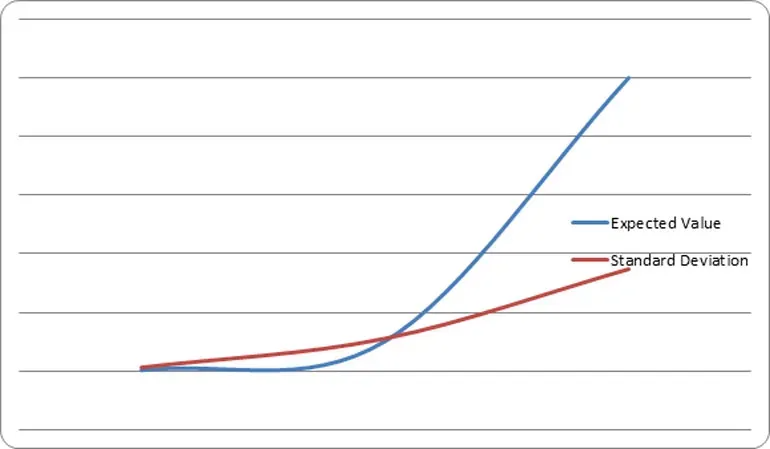
À medida que o número de eventos aumenta, o desvio padrão fica mais pequeno relativamente ao valor esperado. Algures ao longo da curva, o valor esperado e o desvio padrão cruzam-se.
E é nesse momento que há uma probabilidade de 84% do desvio padrão ser menor do que o valor esperado. Isto dá uma probabilidade de 84% de ter lucro. Quando o número de eventos aumenta além desse ponto, a percentagem aumenta logaritmicamente. Isso é demonstrado pictoricamente no gráfico seguinte.
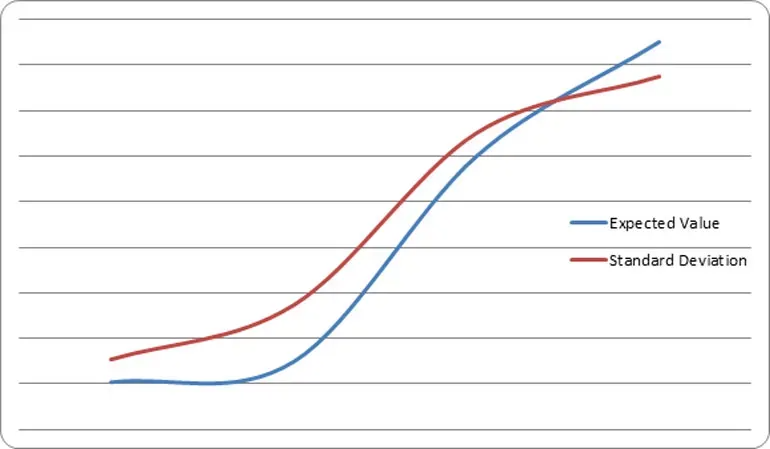
O ponto de interseção entre o valor esperado e o desvio padrão está um pouco abaixo das 12.000 mãos. Às 12.000 mãos, há uma probabilidade de 83% do valor esperado ultrapassar o desvio padrão negativo, indicando um EV positivo 84% das vezes.
Quando a vantagem geral aumenta, o ponto de “equivalência”, ou o número de mãos em que o valor esperado é igual ao desvio padrão, é alcançado em menos mãos. Calculando o mesmo gráfico com 2% de vantagem, o gráfico mostra um ponto de equivalência de 5.600 mãos.
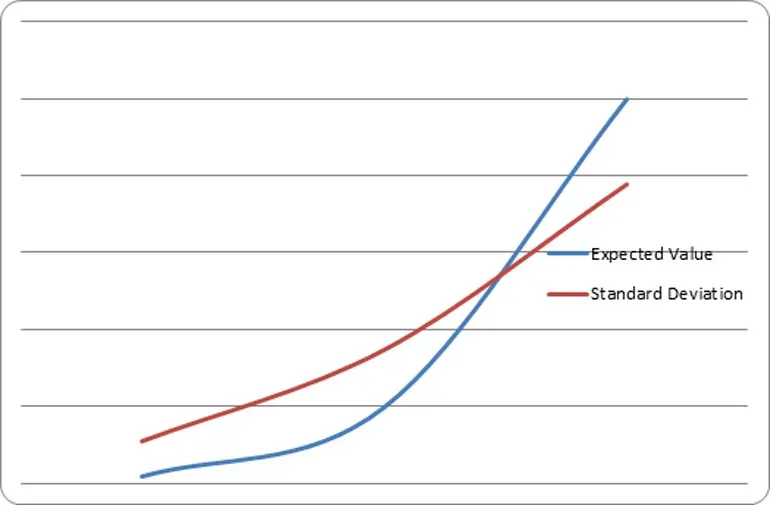
Aumentar uma Vantagem
A forma mais eficaz de aumentar uma vantagem é ter um spread de apostas alto. Num cenário ideal, um jogador aposta muito quando há vantagem e nada quando não há vantagem.
Imagine um jogo em que quando uma moeda é lançada e o resultado é cara, a pessoa recebe 2 unidades e quando o resultado é coroa, a pessoa tem de pagar 1 unidade. Jogaria esse jogo? A maioria das pessoas diria que sim.
Contudo, tem de garantir que tem unidades suficientes para ultrapassar quaisquer fases negativas pelas quais pode passar. Se uma pessoa apenas tiver 4 unidades para apostar, é possível que o resultado seja coroa 4 vezes seguidas, fazendo com que a pessoa perdesse toda a sua banca. Contudo, se essa mesma pessoa tivesse 100 unidades, teria fundos suficientes para sobreviver às oscilações negativas do jogo, e haveria uma probabilidade muito boa de o jogo ser lucrativo para o jogador.
Nos jogos de casino, são necessários fundos suficientes para sobreviver a quaisquer oscilações negativas que possam ocorrer. No geral, quanto mais fundos você tiver, mais probabilidade de sucesso terá. É por isso que os casinos geralmente duram mais do que os jogadores. Os jogadores nunca são capazes de ganhar no longo prazo e superar as lombas estatísticas pelo caminho.
Originalmente publicado a 6 de Maio de 2023


